*** LOS NUMEROS COMPLEJOS ***

DEFINICIÓN:

El conjunto de los números complejos es el de los números de la forma   z = a + bi, en donde:

El numero a es la parte real de z (R e Z)

El numero bi es la parte imaginaria de z (Im z)

i es la unidad imaginaria

De la definicion de la unidad imaginaria se tiene:

MODULO DE UN NUMERO COMPLEJO

Se define el modulo de un número complejo como el módulo del vector que lo representa, es decir, si z=a+bi, entonces el módulo de z es:

CONJUGADO DE UN NUMERO COMPLEJO

El conjugado de un número complejo se define como su simétrico respecto del eje real, es decir, si z=a+bi, entonces el conjugado de z es:

SUMA DE NÚMEROS COMPLEJOS

Se llama suma de dos o más números complejos al complejo que tiene como componente real la suma de las componentes reales y como componente imaginaria la suma de las componentes imaginarias de los números sumandos.

ejemplo:

(4+3i)+(2-9i)=  (4+2)+(3-9)i = 6-7i

MULTIPLICACIÓN DE NÚMEROS COMPLEJOs

Sean los numeros complejos z=a+bi   y   q=c+di,

el producto de estos dos numeros esta dado por:

zq=(ab-cd)+(ad+cb)i

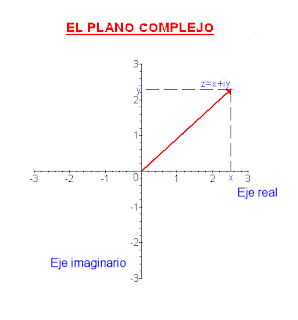
REPRESENTACION EN EL PLANO COMPLEJO